Version:v1.1
Abstract
This article explains the details of Plessey and MSI symbology.
![[Note]](https://www.crifan.com/files/res/docbook/images/note.png) |
This article provide multiple formats: |
|---|---|
|
HTML version online address: http://www.crifan.com/files/doc/docbook/symbology_plessey/release/html/symbology_plessey.html Any question or bug report are encouraged to post in the discussion group: |
2012-08-09
| Revision History | ||
|---|---|---|
| Revision 1.0 | 2011-05-17 | crl |
| ||
| Revision 1.1 | 2012-08-09 | crl |
| ||
Copyright © 2012 Crifan, http://crifan.com
This article conform to:Attribution-NonCommercial 2.5 Generic (CC BY-NC 2.5)
Table of Contents
List of Figures
List of Tables
Table of Contents
Abstract
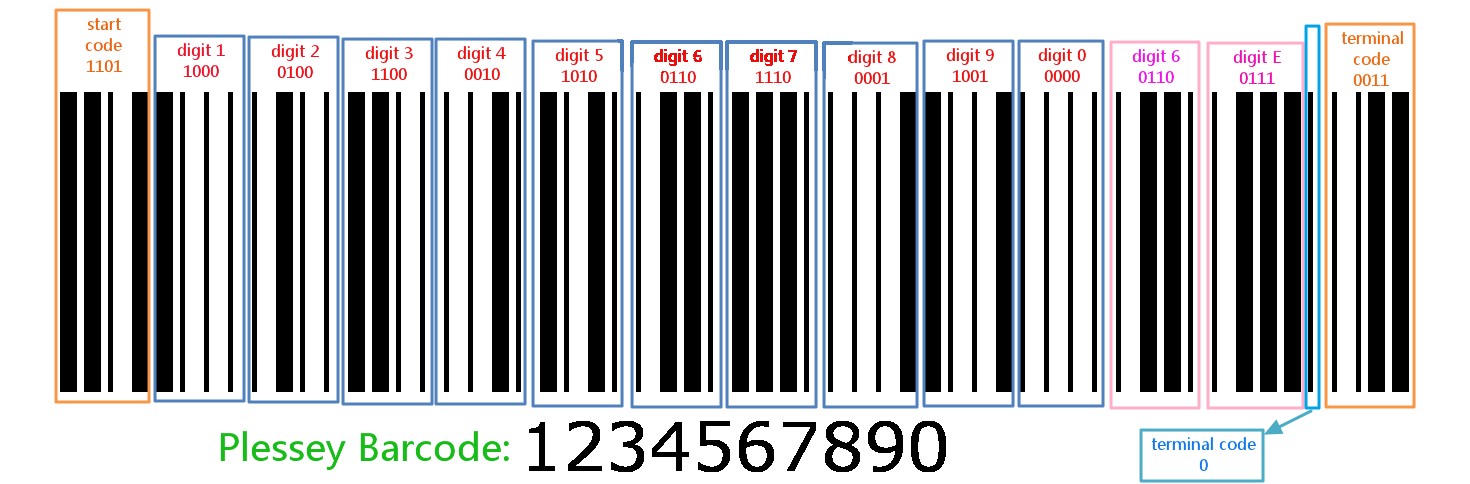
Plessey barcode/code is a 1D linear barcode symbology, based on Pulse Wide Modulation.
Plessey is originally developed in 1971 by The Plessey Company plc, a British-based company. So, sometimes is called “UK Plessey”.
So,
Plessey = UK Plessey
Plessey’s barcode pattern is so simple that, with casual familiarity with the code, you can actually read the bar codes with your eyes.
Plessey basic code rule is:
- Wide bar following by narrow space is a "1" bit.
- Narrow bar followed by wide space is a "0" bit.
And each digit number is represented by four bit.
If you only calculate the bar (horizontal black line), the wide bar means ‘1’ and the narrow bar means ‘0’.
So, the digit ‘1’:
- BCD (Binary- Coded Decimal) is 0001b
- reversed BCD is 1000b
- wide bar + narrow bar + narrow bar + narrow bar
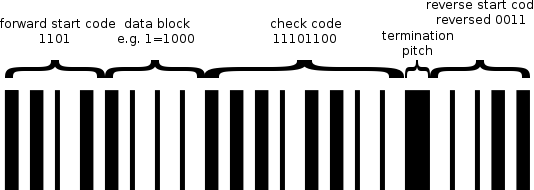
Table 1.1. Plessey Barcode Format
| start character | Any number of labels/characters/digits | Checksum / check digit / code | A stop / termination character / block / pitch bar | the reverse start code |
|---|---|---|---|---|
| 4it =1101 | XXX...(eg, 012345...) | 8bit(eg. 0110 0111) | 1bit=X(eg, 1) | 4bit=0011 |
In which:
- the forward start code
The forward start code is "1101". It defines the beginning of the encoded text.
- the label / data digits
The characters of the text to encode are hexadecimal values encoded as reversed BCD.
Table 1.2. Plessey Bits Encoding Rule
Value Encoding Value Encoding Value Encoding Value Encoding 0 0000 4 0010 8 0001 C 0011 1 1000 5 1010 9 1001 D 1011 2 0100 6 0110 A 0101 E 0111 3 1100 7 1110 B 1101 F 1111
- the check code, for error detection
The check code for error detection and correction is as CRC, using polynomial division.
Is uses 2 characters, or 8 bits.
The generator polynomial is g(x) = x8 + x7 + x6 + x5 + x3 + 1 with n=8, in binary "111101001".
- the termination bar
The termination bar follows the CRC. It's a full pitch bar.
- the reverse start code
The reverse start code, with the forward start code, are used to detect the direction of reading : from left to right or right to left.
It's encoded as a reversed "0011".
Reversed because the "0" is represented by a wide space and simple bar, and "1" as a simple space and wide bar.
The chief advantages are the relative ease of printing using the dot-matrix printers popular at the time of the code's introduction, and its somewhat higher density than the more common 2 of 5 and 3 of 9 codes.
It is one of the first barcode symbology, and is still used in some rare libraries and for shelf tags in retail stores, in part as a solution to their internal requirement for stock control.
The Plessey was first used in the early 1970s by J.Sainsbury to identify all of its products on supermarket shelves for its product restocking system.
However, Plessey does not encode numbers efficiently, and other characteristics of the language make it one of the most error-prone of all bar code languages.
Accordingly, the MSI company came out with a revised standard for the Plessey language (now called MSI Plessey, also known as Plessey modified) which employed a second check digit. This improved the reliability of the language enough so that the MSI version of the code has continued in use in specialty applications.
Except the MSI, several other variations of Plessey is Anker Code by ADS Company, Telxon. It is difficult to have the specifications for them nowadays and thus hard to tell the differences between them (except for MSI), because is was mainly available as paper document and in discontinued since then.
Table of Contents
Abstract
MSI Plessey is a barcode symbology, is a variation of Plessey, is the most widely supported variation of Plessey.
Also called “Modified Plessey”, or MSI.
So:
MSI = MSI Plessey = Modified Plessey
Following description will use MSI.
MSI was developed by the MSI Data Corporation, based on the original Plessey Code, Currently maintained by Symbol Technologies, Inc.
While the length of an MSI bar code can be of any length, a given application usually implements a fixed-length code
MSI is a continuous symbology that is not self-checking, based on Pulse-Width Modulation
The MSI character set consist of the numbers 0..9 as well as two "guard" characters (representing the beginning and end of the barcode).
So, like Interleaved 2-of-5 and UPC, MSI is an all-numeric language, not support alphabetic characters.
The bit representation is same with Plessey:
- Wide bar following by narrow space is a "1" bit.
- Narrow bar followed by wide space is a "0" bit.
But the digit representation is more simple:
Each digit number is represented by four bit.
Except the start and stop bits, If you only calculate the bar (horizontal black line), the wide bar means ‘1’ and the narrow bar means ‘0’,
then it is the same rule as using binary to represent the digit:
Digit 0 = 0000b
Digit 1 = 0001b
Digit 2 = 0010b
Digit 3 = 0011b
...
Table 2.1. MSI Barcode Format
| Format | start character | Any number of digits | Checksum digit(s) | A stop character |
|---|---|---|---|---|
| Explanation | a wide bar followed by a narrow space | Digits | 5 modes:
|
narrow bar, a wide space, then a narrow bar |
| Digits/Bits | Bit: 1 | Digits: XXX... | Digit(s): X/XX | Bits: 00 |
The MSI barcode uses one of five possible schemes for calculating a check digit:
- No check digit (least common)
- Mod 10 (most common)
- Mod 11
- Mod 1010
- Mod 1110
The checksum algorithm for Mode 10 is to use “Luhn algorithm”:
- Counting from the check digit, which is the rightmost one, and moving left, double (x 2) the value of every second digit.
- Sum the digits of the products (eg, 10 ⇒ 1+0 = 1, 14 ⇒ 1+ 4 =5) together with the un-doubled digits from the original number
- Got the sum, then do: sum Mod 10 = check digit
Assume an example of an account number "1234567" that will have a check digit added, making it of the form “1234567X”:
Then the steps to calculate the X are:
Table 2.2. Mode 10 Check Digit Example
| Example | 1 | 2 | 3 | 4 | 5 | 6 | 7 | Mode 10 Check digit |
|---|---|---|---|---|---|---|---|---|
| (1) Append X | 1 | 2 | 3 | 4 | 5 | 6 | 7 | X |
| (2) From rightmost, every second digit × 2 | 2 | 6 | 10 | 14 | ||||
| (3) List all | 2 | 2 | 6 | 4 | 1+0 | 6 | 1+4 | |
| (4) Got Summary | Sum=2+2+6+4+1+0+6+1+4=26, 26 Mod 10 = 4 | X = 4 | ||||||
| (5)Result | 12345674 | |||||||
For the second checksum digit, the calculation method is still the same, just take the “12345674” as the input number, the calculate the X for “12345674X”
To calculate the Modulo 11 check digit, use the following process:
- Assign a weight to each character in the code, starting with a weight of 2 in the right-most position and incrementing by one as you move to the left. After you reach a weight of 7, the next digit will have a weight of 2 (that is, weighting goes from 2 to 7 and then wraps around back to 2)
- Multiply the value of each character by its weight, and sum the result of all the characters
- Perform a modulo 11 on the result (sum) of step 2
Assume an example of an account number "1234567" that will have a mode 11 check digit added, making it of the form “1234567X”:
Table 2.4. Mode 11 Check Digit Example
| Example | 1 | 2 | 3 | 4 | 5 | 6 | 7 | Mode 11 Check digit |
|---|---|---|---|---|---|---|---|---|
| (1) Add weight | 2 | 7 | 6 | 5 | 4 | 3 | 2 | X |
| (2) digit × weight | 2 | 14 | 18 | 20 | 20 | 18 | 14 | |
| (3)add all, get sum | Sum=2+14+18+20+20+18+14=106, 106 Mod 11 = 4 | X = 4 | ||||||
| (4)Result | 12345674 | |||||||
And for the mode 1110, take “1234567”as example, just to use the mode 11 for “1234567”to calculate the first mode 11 check digit, is 4, then do mode 10 for “12345674”then calculate out the second mode 10 check digit, is 1, so the whole result is “123456741”
![[Tip]](https://www.crifan.com/files/res/docbook/images/tip.png) |
Tip |
|---|---|
While most MSI barcodes include at least one checksum digit, so in many case, the printed MSI barcode does not show out the first checksum digit, while only show the second checksum digit if exists. |
MSI is used primarily for inventory control, marking storage containers and shelves in warehouse environments.
MSI, and other symbologies based on Pulse-Width Modulation, offer no significant benefit over more modern symbologies. While it is not a bad idea to support MSI for legacy bar codes, most new applications do not choose MSI as their symbology of choice.