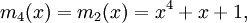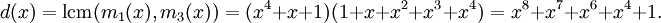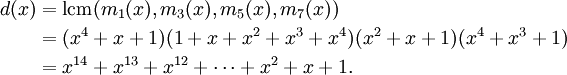BCH code

From Wikipedia, the free encyclopedia

In coding theory the BCH codes form a class of parameterised error-correcting codes which have been the subject of much academic attention in the last fifty years. BCH codes were invented in 1959 by Hocquenghem, and independently in 1960 by Bose and Ray-Chaudhuri^[1]. The acronym BCH comprises the initials of these inventors’ names.

The principal advantage of BCH codes is the ease with which they can be decoded, via an elegant algebraic method known as syndrome decoding. This allows very simple electronic hardware to perform the task, obviating the need for a computer, and meaning that a decoding device may be made small and low-powered. As a class of codes, they are also highly flexible, allowing control over block length and acceptable error thresholds, meaning that a custom code can be designed to a given specification (subject to mathematical constraints).

In technical terms a BCH code is a multilevel, cyclic, error-correcting, variable-length digital code used to correct multiple random error patterns. BCH codes may also be used with multilevel phase-shift keying whenever the number of levels is a prime number or a power of a prime number. A BCH code in 11 levels has been used to represent the 10 decimal digits plus a sign digit.^[2]

[hide]

[edit] Construction

A BCH code is a polynomial code over a finite field with a particularly chosen generator polynomial. It is also a cyclic code as well.

[edit] Simplified BCH codes

For ease of exposition, we first describe a special class of BCH codes. General BCH codes are described in the next section.

Definition. Fix a finite field $G F (q)$ , where $q$ is a prime power. Also fix positive integers $m$ , $n$ , and $d$ such that $n = q m - 1$ and $2 leq d leq n$ . We will construct a polynomial code over $G F (q)$ with code length $n$ , whose minimum Hamming distance is at least $d$ . What remains to be specified is the generator polynomial of this code.

Let $α$ be a primitive $n$ th root of unity in $G F (q m)$ . For all $i$ , let $m i (x)$ be the minimal polynomial of $α i$ with coefficients in $G F (q)$ . The generator polynomial of the BCH code is defined as the least common multiple $g(x) = {rm lcm}(m_1(x),ldots,m_{d-1}(x))$ .

[edit] Example

Let $q = 2$ and $m = 4$ (therefore $n = 15$ ). We will consider different values of $d$ . There is a primitive root $alphain GF(16)$ satisfying

α 4 + α + 1 = 0

(1);

its minimal polynomial over $G F (2)$ is : $m 1 (x) = x 4 + x + 1$ . Note that in $G F (2)$ , the equation $(a + b) 2 = a 2 + 2 a b + b 2 = a 2 + b 2$ holds, and therefore $m 1 (α 2) = m 1 (α) 2 = 0$ . Thus $α 2$ is a root of $m 1 (x)$ , and therefore

m 2 (x) = m 1 (x) = x 4 + x + 1

To compute $m 3 (x)$ , notice that, by repeated application of (1), we have the following linear relations:

$1 = 0α 3 + 0α 2 + 0α + 1$
$α 3 = 1α 3 + 0α 2 + 0α + 0$
$α 6 = 1α 3 + 1α 2 + 0α + 0$
$α 9 = 1α 3 + 0α 2 + 1α + 0$
$α 12 = 1α 3 + 1α 2 + 1α + 1$

Five right-hand-sides of length four must be linearly dependent, and indeed we find a linear dependency $α 12 + α 9 + α 6 + α 3 + 1 = 0$ . Since there is no smaller degree dependency, the minimal polynomial of $α 3$ is : $m 3 (x) = x 4 + x 3 + x 2 + x + 1$ . Continuing in a similar manner, we find

$m_4(x) = m_2(x) = x^4+x+1,,$

$m_5(x) = x^2+x+1,,$

$m_6(x) = m_3(x) = x^4+x^3+x^2+x+1,,$

$m_7(x) = x^4+x^3+1.,$

The BCH code with $d = 1,2,3$ has generator polynomial

$d(x) = m_1(x) = x^4+x+1.,$

It has minimal Hamming distance at least 3 and corrects up to 1 error. Since the generator polynomial is of degree 4, this code has 11 data bits and 4 checksum bits.

The BCH code with $d = 4,5$ has generator polynomial

$d(x) = {rm lcm}(m_1(x),m_3(x)) = (x^4+x+1)(1+x+x^2+x^3+x^4) = x^8+x^7+x^6+x^4+1.,$

It has minimal Hamming distance at least 5 and corrects up to 2 errors. Since the generator polynomial is of degree 8, this code has 7 data bits and 8 checksum bits.

The BCH code with $d = 6,7$ has generator polynomial

$begin{align}d(x) & {} = {rm lcm}(m_1(x),m_3(x),m_5(x)) \& {} = (x^4+x+1)(1+x+x^2+x^3+x^4)(x^2+x+1) \& {} = x^{10}+x^8+x^5+x^4+x^2+x+1.end{align}$

It has minimal Hamming distance at least 7 and corrects up to 3 errors. This code has 5 data bits and 10 checksum bits.

The BCH code with $d = 8$ and higher have generator polynomial

$begin{align}d(x) & {} = {rm lcm}(m_1(x),m_3(x),m_5(x),m_7(x)) \& {} = (x^4+x+1)(1+x+x^2+x^3+x^4)(x^2+x+1)(x^4+x^3+1) \& {} = x^{14}+x^{13}+x^{12}+cdots+x^2+x+1.end{align}$

This code has minimal Hamming distance 15 and corrects 7 errors. It has 1 data bit and 14 checksum bits. In fact, this code only has two codewords 000000000000000 and 111111111111111.

[edit] General BCH codes

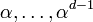General BCH codes differ from the simplified case discussed above in two respects. First, one replaces the requirement $n = q m - 1$ by a more general condition. Second, the consecutive roots of the generator polynomial may run from $alpha^c,ldots,alpha^{c+d-2}$ instead of $alpha,ldots,alpha^{d-1}$ .

Definition. Fix a finite field $G F (q)$ , where $q$ is a prime power. Chose positive integers $m, n, d, c$ such that 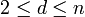$2leq dleq n$ , $gcd(n, q) = 1$ , and $m$ is the multiplicative order of $q$ modulo $n$ .

As before, let $α$ be a primitive $n$ th root of unity in $G F (q m)$ , and let $m i (x)$ be the minimal polynomial over $G F (q)$ of $α i$ for all $i$ . The generator polynomial of the BCH code is defined as the least common multiple $g(x) = {rm lcm}(m_c(x),ldots,m_{c+d-2}(x))$ .

Note: if $n = q m - 1$ as in the simplified definition, then $gcd(n, q)$ is automatically 1, and the order of $q$ $m$ modulo $n$ is automatically $m$ . Therefore, the simplified definition is indeed a special case of the general one.

[edit] Properties

Property. The generator polynomial of a BCH code has degree at most $(d - 1) m$ . Moreover, if $q = 2$ and $c = 1$ , the generator polynomial has degree at most $d m / 2$ .

Proof: each minimal polynomial $m i (x)$ has degree at most $m$ . Therefore, the least common multiple of $d - 1$ of them has degree at most $(d - 1) m$ . Moreover, if $q = 2$ , then $m i (x) = m 2 i (x)$ for all $i$ . Therefore, $g (x)$ is the least common multiple of at most $d / 2$ minimal polynomials $m i (x)$ for odd indices $i$ , each of degree at most $m$ .

Property. A BCH code has minimal Hamming distance at least $d$ .

Proof: We only give the proof in the simplified case; the general case is similar. Suppose that $p (x)$ is a code word with fewer than $d$ non-zero terms. Then

$p(x) = b_1x^{j_1} + cdots + b_{d-1}x^{j_{d-1}},text{ where }j_1<j_2<cdots<j_{d-1}.$

Recall that $alpha^1,ldots,alpha^{d-1}$ are roots of $g (x)$ , hence of $p (x)$ . This implies that $b_1,ldots,b_{d-1}$ satisfy the following equations, for $i=1,ldots,d-1$ :

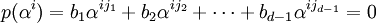$p(alpha^i) = b_1alpha^{ij_1} + b_2alpha^{ij_2} + cdots + b_{d-1}alpha^{ij_{d-1}} = 0$ .

Dividing this by 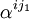$alpha^{ij_1}$ , and writing $k l = j l - j 1$ , we get

$b_1 + b_2alpha^{ik_2} + cdots + b_{d-1}alpha^{ik_{d-1}} = 0$

for all $i$ , or equivalently

$begin{bmatrix}1 & alpha^{k_2} & cdots & alpha^{k_{d-1}} \1 & alpha^{2k_2} & cdots & alpha^{2k_{d-1}} \vdots & vdots && vdots \1 & alpha^{(d-1)k_2} & cdots & alpha^{(d-1)k_{d-1}} \end{bmatrix}begin{bmatrix}b_1 \ b_2 \ vdots \ b_{d-1}end{bmatrix}=begin{bmatrix}0 \ 0 \ vdots \ 0end{bmatrix}$

This matrix is seen to be a Vandermonde matrix, and its determinant is

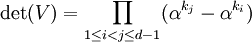$det(V) = prod_{1le i<jle d-1} (alpha^{k_j}-alpha^{k_i})$ ,

which is non-zero. It therefore follows that $b_1,ldots,b_{d-1}=0$ , hence $p (x) = 0$ .

Property. A BCH code is cyclic.

Proof: A polynomial code of length $n$ is cyclic if and only if its generator polynomial divides $x n - 1$ . Since $g (x)$ is the minimal polynomial with roots $alpha^c,ldots,alpha^{c+d-2}$ , it suffices to check that each of $alpha^c,ldots,alpha^{c+d-2}$ is a root of $x n - 1$ . This follows immediately from the fact that $α$ is, by definition, an $n$ th root of unity.

[edit] Special cases

A BCH code with $c = 1$ is called a narrow-sense BCH code.
A BCH code with $n = q m - 1$ is called primitive.

Therefore, the "simplified" BCH codes we considered above were just the primitive narrow-sense codes.

A narrow-sense BCH code with $n = q - 1$ is called a Reed-Solomon code.

[edit] Decoding

BCH decoding is split into the following four steps

Calculate the 2t syndrome values, for the received vector R
Calculate the error locator polynomials
Calculate the roots of this polynomial, to get error location positions.
If non-binary BCH, Calculate the error values at these error locations.

The following steps are illustrated below. Suppose we receive a codeword vector $r$ (the polynomial $R (x)$ ).

If there is no error $R (α) = R (α 3) = 0$

If there is one error (i.e. $r = c + e i$ where $e i$ represents the $i t h$ basis vector for $mathbb{R}^{14}$ .

So then

S 1 = R (α) = C (α) + α i = α i

$S_3 = R(alpha^3) =C(alpha^3) + (alpha^3)^i =(alpha^i)^3 =S_1^3$

so we can recognize one error. A change in the bit position shown by $α$ ‘s power will aid us correct that error.

If there are two errors

r = c + e i + e k

then

S 1 = R (α) = C (α) + α i + α k

S 3 = R (α 3) = C (α 3) + (α 3) i + (α 3) k = (α 3) i + (α 3) k

which is not the same as 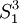$S_1^3$ so we can recognize two errors. Further algebra can aid us in correcting these two errors.

Original source (first two paragraphs) from Federal Standard 1037C

The above text has been taken from: http://bch-code.foosquare.com/

[edit] BCH decoding algorithms

Popular decoding algorithms are,

Peterson Gorenstein Zierler algorithm
Berlekamp-Massey algorithm

[edit] Peterson Gorenstein Zierler algorithm

[edit] Assumptions

Peterson’s algorithm, is the step 2, of the generalized BCH decoding procedure. We use Peterson’s algorithm, to calculate the error locator polynomial coefficients $lambda_1 , lambda_2, dots, lambda_{2t}$ of a polynomial $Lambda(x) = 1 + lambda_1 x + lambda_2 x^2 + cdots + lambda_{2t}x^{2t}$

Now the procedure of the Peterson Gorenstein Zierler algorithm, for a given $(n, k, d m i n)$ BCH code designed to correct $[t=frac{d_{min}-1}{2}]$ errors, is

[edit] Algorithm

First generate the Matrix of $2 t$ syndromes,
Next generate the 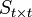$S_{ttimes t}$ matrix with the elements, syndrome values,

$S_{t times t}=begin{bmatrix}s_1&s_2&s_3&dots&s_t\s_2&s_3&s_4&dots&s_{t+1}\s_3&s_4&s_5&dots&s_{t+2}\dots&dots&dots&dots&dots\s_t&s_{t+1}&s_{t+2}&dots&s_{2t-1}end{bmatrix}$

Generate a $c t x 1$ matrix with, elements,

$C_{t times 1}=begin{bmatrix}s_{t+1}\s_{t+2}\vdots\vdots\s_{2t}end{bmatrix}$

Let $Λ$ denote the unknown polynomial coefficients, which are given,using

$Lambda_{t times 1} = begin{bmatrix}lambda_{1}\lambda_{2}\lambda_{3}\lambda_{4}\vdots\lambda_{t}end{bmatrix}$

Form the matrix equation

$S_{t times t} Lambda_{t times 1} = C_{t times 1,}$

If the determinant of matrix 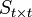$S_{t times t}$ exists, then we can actually, find an inverse of this matrix, and solve for the values of unknown $Λ$ values.

If $det(S_{t times t}) = 0$ , then follow

if <span class="texhtml"><em>t</em> = 0</span>
       then
             declare an empty error locator polynomial
             stop Peterson procedure.
       end
       set <img class="tex" alt="t leftarrow t -1" src="http://upload.wikimedia.org/math/0/3/5/035d13347fad3d7b0014c5da2503aaf7.png" />
       continue from the beginning of Peterson's decoding

After you have values of $Λ$ you have with you the error locator polynomial.
Stop Peterson procedure.

[edit] Factoring error locator polynomial

Now that you have $Λ(x)$ polynomial, you can find its roots in the form $Lambda(x)=(alpha^i x + 1) (alpha ^j x + 1) cdots (alpha^k x + 1)$ using, the Chien search algorithm. The exponential powers of the primitive element $α$ , will yield the positions where errors occur in the received word; hence the name ‘error locator’ polynomial.

[edit] Correcting errors

For the case of binary BCH, you can directly correct the received vectors, at the positions of the powers of primitive elements, of the error locator polynomial factors. Finally, just flip the bits for the received word, at these positions, and we have the corrected code word, from BCH decoding.

We may also use Berlekamp-Massey algorithm for determining the error locator polynomial, and hence solve the BCH decoding problem.

[edit] Simulation results

The simulation results for a AWGN BPSK system using a (63,36,5) BCH code are shown in this figure. A coding gain of almost 2 dB is observed at a bit error rate $10 - 3$ .

[edit] Citations

^ Page 189, Reed, Irving, S.. Error-Control Coding for Data Networks. Kiuwer Academic Publishers. ISBN 0-7923-8528-4.
^ Federal Standard 1037C, 1996.

[edit] References

S. Lin and D. Costello. Error Control Coding: Fundamentals and Applications. Prentice-Hall, Englewood Cliffs, NJ, 2004.
Galois Field Calculator: http://www.geocities.com/myopic_stargazer/gf_calc.zip
W.J. Gilbert and W.K. Nicholson. Modern Algebra with Applications, 2nd edition. Wiley, 2004.
R. Lidl and G. Pilz. Applied Abstract Algebra, 2nd edition. Wiley, 1999.

Retrieved from "http://en.wikipedia.org/wiki/BCH_code"

转载请注明：在路上 » BCH code

Post Views: 2,211

BCH code

BCH code

From Wikipedia, the free encyclopedia

Contents

[edit] Construction

[edit] Simplified BCH codes

[edit] Example

[edit] General BCH codes

[edit] Properties

[edit] Special cases

[edit] Decoding

[edit] BCH decoding algorithms

[edit] Peterson Gorenstein Zierler algorithm

[edit] Assumptions

[edit] Algorithm

[edit] Factoring error locator polynomial

[edit] Correcting errors

[edit] Simulation results

[edit] Citations

[edit] References

与本文相关的文章

Hi，您需要填写昵称和邮箱！